Как работает математическое ожидание в ставках

И почему без его оценки не достичь успеха на большой дистанции.

Один из основополагающих принципов ставок на спорт гласит, что дистанция — важнейший показатель успешности: конкретный подход может казаться профитным после десяти совершённых ставок, но уже после 100 пари игрок может залезть в солидный минус. 

Для оценки профитности каждой конкретной ставки на дистанции на помощь приходит математика, а точнее один из её важнейших разделов — статистика: математическое ожидание позволяет игроку оценить жизнеспособность ставки на дистанции без необходимости «обкатывать» её на практике.

Остановимся подробнее на математическом ожидании и на том, как оно помогает грамотно распределять банк. 

Математическое ожидание: инструкция к применению 

Математическое ожидание — это величина, указывающая на среднее значение случайной величины. То есть как раз математическое ожидание указывает на то, насколько профитным окажется выбранный исход на дистанции, отталкиваясь от его вероятности.

Иначе говоря, чистый размер выигрыша необходимо умножить на процент вероятности и отнять от полученного числа произведение суммы ставки и обратной вероятности. Сложно?! Разберёмся на конкретном примере. 

Беттор собирается ставить на ТБ 2,5 в матчах Уэльса, который как раз совсем скоро встретится в квалификации к чемпионату мира-2022 с Австрией. Коэффициент на выбранный исход в предстоящем матче 2.54, то есть вероятность его свершения составляет около 39%, а поставить игрок планирует 1000 тенге.

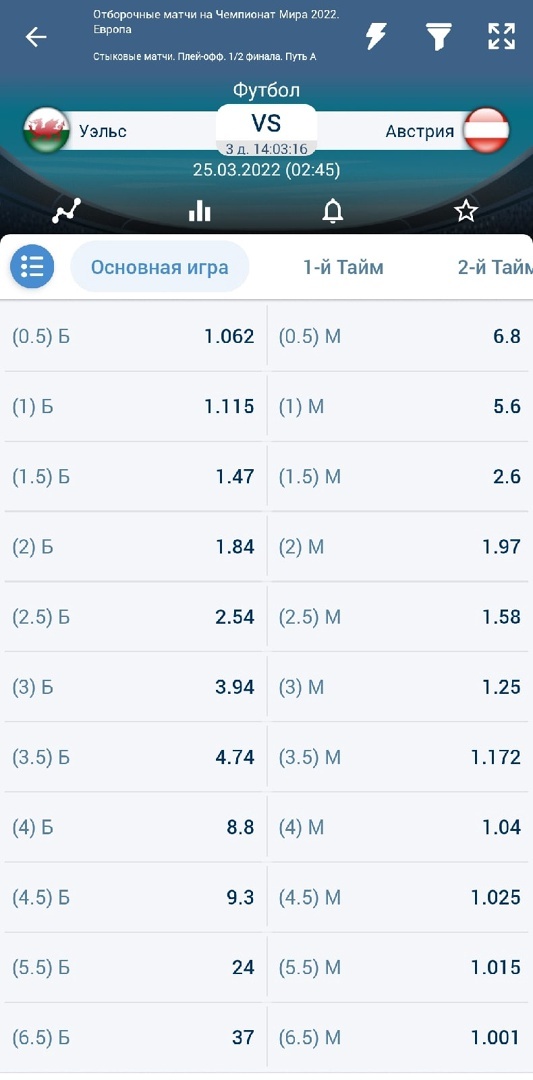
Подставляем значения в формулу: 1540*0,39–1000*0,61 = –9,4. Это говорит о том, что, исходя из теории вероятностей, на дистанции подобный подход неизменно приведёт игрока в минус. 

Сразу оговоримся: отрицательное математическое ожидание не означает, что Уэльс с Австрией в очном противостоянии не забьют больше трёх мячей — шанс на это 39%, а значит, соперники вполне могут выдать результативную встречу. 

Отрицательный результат лишь указывает на тот факт, что на длительной дистанции подход обязательно приведёт в минус. Именно поэтому использовать формулу математического ожидания целесообразно по отношению лишь к тем исходам, на которые беттор решил ставить систематически.

На вероятность больших и средних рынков влияет слишком большое количество факторов, в том числе тех, которые трудно выразить математически: атмосфера в команде, форма отдельных исполнителей и так далее. Однако при наличии системного подхода оценка математического ожидания поможет игроку грамотно оценить риски и отбросить заведомо минусовые варианты. 

Дисперсия и банкролл-менеджмент

Дисперсия — это мера разброса случайной величины относительно её математического ожидания на конкретном отрезке. Иными словами, даже при положительном математическом ожидании на отдельных отрезках игрок может уходить в минус, причём чем больше сумма флэта и количество ставок, тем сильнее может просесть результат. 

Именно поэтому большинство профессиональных игроков и советуют ограничить свой флэт 3-5% от банкролла, иначе просадка может заметно ударить и по кошельку, и по морали игрока. Именно эта зависимость дисперсии от банкролла открывает перед беттором два варианта игры — с низкой и высокой дисперсией. 

В первом случае ставочник играет максимально аккуратно: не задирает размер флэта, ставит только на те исходы, в которых максимально уверен, а при малейших сомнениях отказывается от пари. Количество ставок в этом случае заметно уменьшается, а небольшая относительно общего банка сумма флэта позволяет сравнительно безболезненно проходить через любые просадки.

Игра с высокой дисперсией подразумевает заключение пари на откровенно рискованные исходы с целью получения большего профита, однако обратной стороной медали являются риск проигрыша весомой части банка и попадание в тильт, от чего не застрахованы даже опытные игроки. 

Математическое ожидание — не гарант успеха

Математическое ожидание не может служить гарантом успеха сразу по двум причинам. О первой мы уже поговорили — это дисперсия, которая при агрессивном подходе к банкролл-менеджменту может привести игрока к потере банка даже при положительном ожидании подхода. 

Вторая причина заключается в том, что спорт — система непостоянная и очень динамичная, поэтому подход, показывавший себя с лучшей стороны ещё вчера, завтра способен оказаться нежизнеспособным ввиду ряда причин: будь то изменение регламента соревнования, тренерские перестановки и многое-многое другое. 

Однако расчёт математического ожидания может быть полезен каждому беттору, как минимум потому что: 

1. Позволяет заранее отмести заведомо минусовые подходы к ставкам.

2. Даёт возможность оценить профитность каждого подхода — не ожидать большого плюса там, где его быть не может.

3. Помогает грамотно распределить банк. 

Математическое ожидание, как и в целом статистика, — один из главных помощников беттора на пути к успеху. Важно лишь не забывать о дисперсии и дисциплинированно переживать просадки.

Читайте также: